In the context of micro-task crowdsourcing, each task is usually performed by several workers. This allows researchers to leverage measures of the agreement among workers on the same task, to estimate the reliability of collected data and to better understand answering behaviors of the participants.

While many measures of agreement between annotators have been proposed, they are known for suffering from many problems and abnormalities. In this work, we identify the main limits of the existing agreement measures in the crowdsourcing context, both by means of toy examples as well as with real-world crowdsourcing data, and propose a novel agreement measure based on probabilistic parameter estimation which overcomes such limits. We validate our new agreement measure and show its flexibility as compared to the existing agreement measures.

CURRENT AGREEMENT MEASURES ARE INADEQUATE

The majority of agreement measures is borrowed from data reliability theory, where the reliability of a set of grouped measurements is assessed via a comparison between the inter-group and the intra-group variability, and where typically the judgments are made by a fixed set of assessors. In the context of crowdsourcing,
these measures suffer from many problems when used to estimate agreement instead of data reliability:

1. The variability of the judgments is typically higher when the judgments concentrate around the center of the scale. This problem is intrinsic to finite scale judgments and can lead to overestimating disagreement over items where the truth concentrates around the scale boundaries.
2. The values around which the judgments concentrate (if any) can be different item by item. This can lead to overestimating expected disagreement and thus increasing the possibility of considering the data as random.
3. For some items a ground truth (e.g., `gold questions’ in crowdsourcing) might be present, that is a value around which judgments are expected to concentrate. This information is typically not used by classic agreement measures.
4. The global variability-based correction by chance leads to many idiosyncrasies in the existing measures, making them hard to use in a crowdsourcing setting.

Our goal in this paper is to address the aforementioned issues, and to build a framework more suitable to estimate worker agreement over a group of tasks in a crowdsourcing context.

OUR MODEL

The intuition behind Φ is connected with the definition of agreement: we consider as agreement the amount of concentration around a data value. Conversely, if the data does not concentrate around a value then we have disagreement (negative agreement in our measure), that can be more or less strong depending on how polarized the different opinions are.
More in detail, our approach can be described as fitting a distribution to the histogram of the judgments and then measuring the dispersion of such distribution.
It is important to notice that the fitting distribution has to be general enough to capture the main behaviors that might occur: flat (random judgments), bell-shaped (agreement), J-shaped (agreement around a value on the boundary of the scale), and U shaped distribution (disagreement), as shown in the following figure.

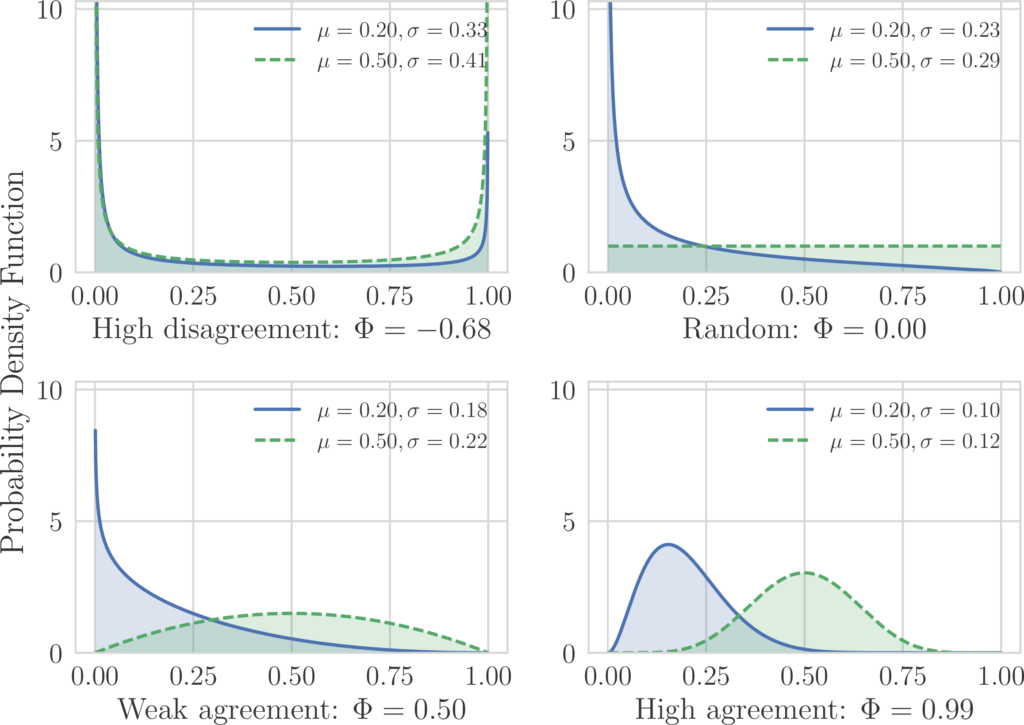
At the same time, the desired distribution has to have a minimal number of parameters, to avoid overfitting. For this reason, we use a Beta distribution to perform the fit: Φ is a transformed parameter of the Beta distribution over the histogram of the collected answers. Such parameter is related to the standard deviation of the fitted distribution, with the difference that here we account for the finiteness of the rating scale, and thus we adjust for the tendency of having lower dispersion when the data concentrates around a value on the boundaries of the rating scale. For example, if we imagine a scenario where assessors add a random Gaussian noise to the ground truth when making a judgment, we can immediately see that the dispersion will be minimum when the ground truth is on the boundary of the scale, because a Gaussian noise that would result is a judgment outside the boundary would be clipped.

The strength of our approach becomes apparent when applied to a group of items to be judged: in the case of relevance judgment tasks, each item i is allowed to have a different average relevance value, while the agreement among workers is defined as the common Φ that better explains the judgment data.
This allows to solve the problems that arise, in the other agreement measures, when trying to correct by chance by using the dispersion of the whole dataset as normalizing factor.

EXAMPLE

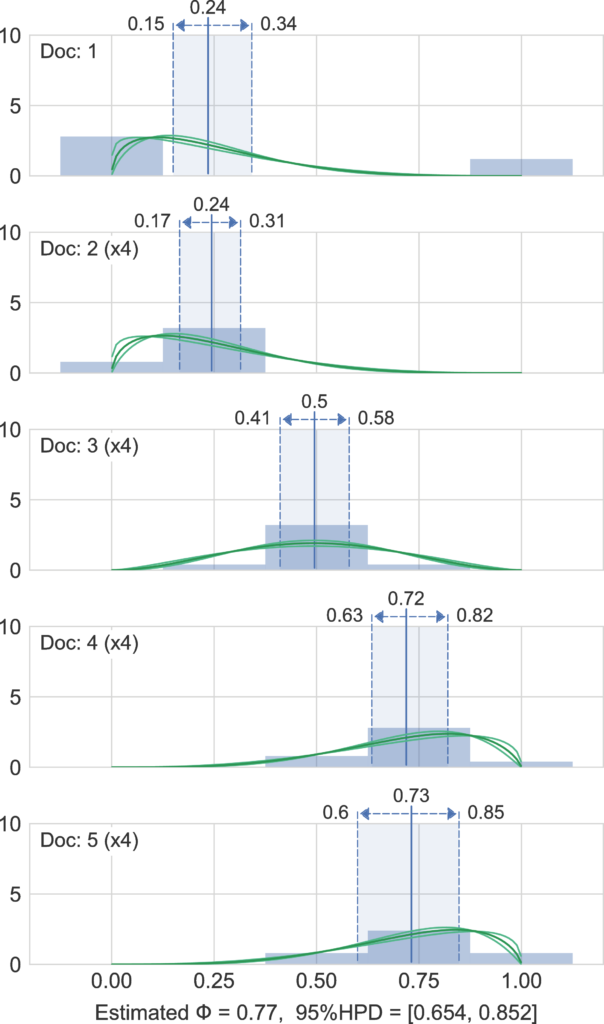
In the following figure we show a representation of the inference results for the judgments of 17 documents. We generated a small synthetic dataset, where the first document has an outlier on the right boundary, and the other 16 documents have a clear central agreement. In the figure it can be seen that documents 2-5 are replicated four times to get 16 documents that have higher agreement. We can see that the model is forced to find the best agreement level (dispersion of the Beta distribution) that collectively explain all the data: while document 1 alone would have been fitted with a high disagreement (a U shaped) Beta, the most probable Beta for the model to explain the whole dataset is the one where the first document has an outlier. This reflects the way we perceive the agreement level as humans, especially with a small set of data samples, and allows to get a robust estimation of agreement for group of documents.

ONLINE TOOL

You can test our tool and access the source code at this link.

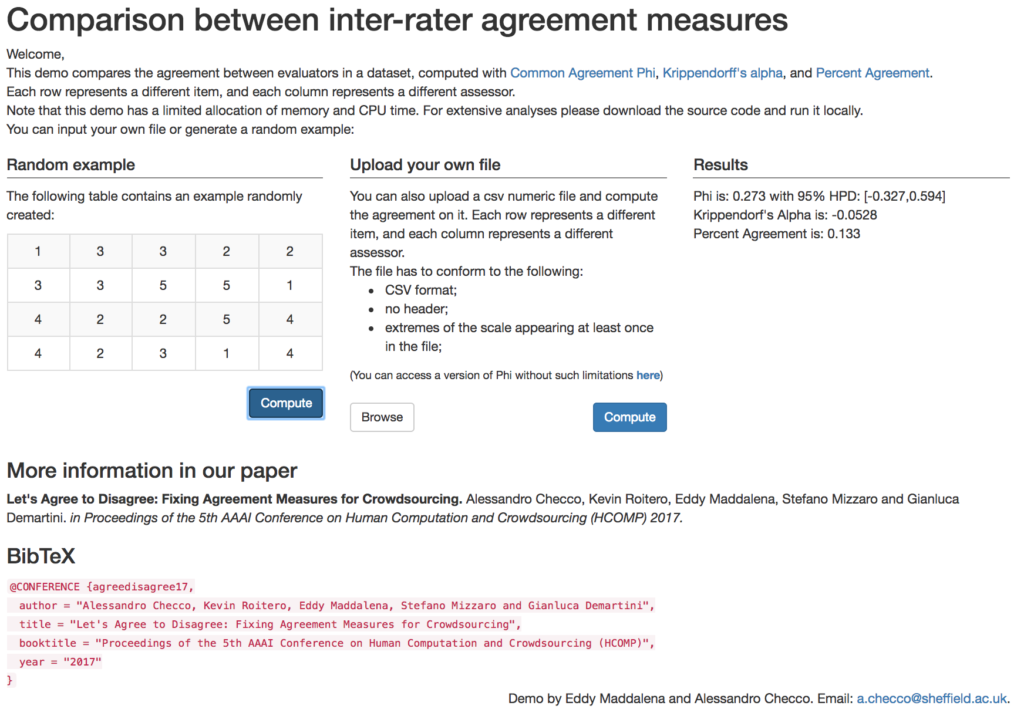
For more information, see our full paper, Let’s Agree to Disagree: Fixing Agreement Measures for Crowdsourcing

Alessandro Checco, Information School, University of Sheffield